akbid-aisyiah-ptk.ac.id – Rumus panjang sisi miring segitiga begitu menarik untuk dikulik. Mengapa demikian? Cari jawabannya di sini!
Memahami rumus panjang sisi miring segitiga merupakan langkah krusial dalam mempelajari geometri. Dalam matematika, sisi miring segitiga, atau kerap disebut hypotenusa, adalah sisi terpanjang segitiga siku-siku. Mengetahui cara menghitung panjang sisi miring ini bukan cuma membantu menyelesaikan berbagai soal matematika, tetapi juga sangat berguna dalam aplikasi praktis sehari-hari, seperti dalam bidang teknik, arsitektur, hingga desain.
Dalam artikel ini, kita akan membahas rumus serta metode yang dipakai untuk menentukan panjang sisi miring segitiga dengan jelas serta mudah dipahami. Dengan pemanfaatan rumus ini, kamu akan mampu menghitung sisi miring lebih tepat, serta memahami bagaimana prinsip dasar geometri diterapkan dalam berbagai situasi praktis. Yuk, mari eksplorasi lebih dalam dan temukan cara yang tepat untuk menentukan panjang sisi miring segitiga!
Rumus Panjang Sisi Miring Segitiga
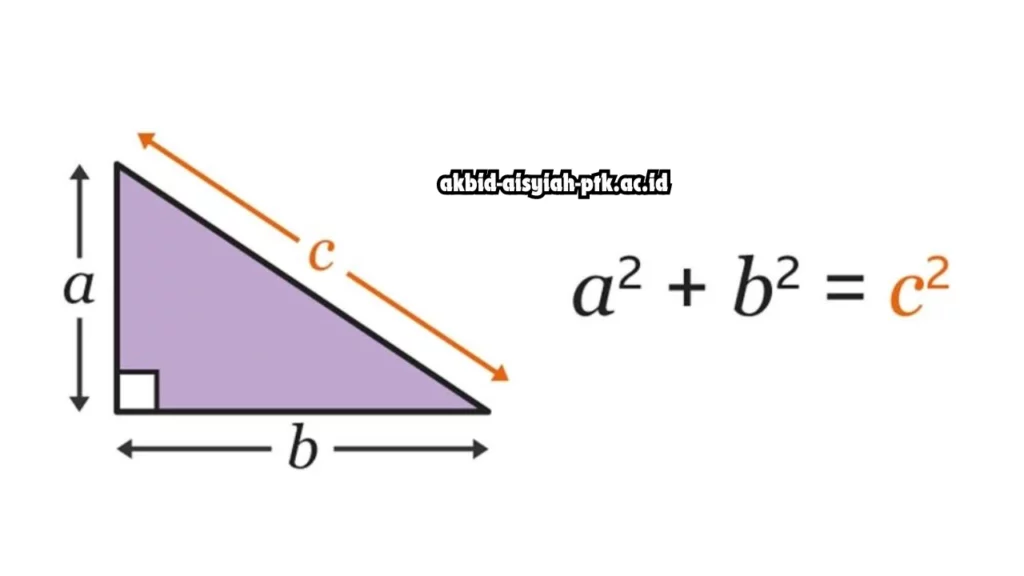
Rumus sisi miring segitiga sangat penting untuk dipahami, terutama segitiga siku-siku. Sisi miring atau hypotenusa merupakan sisi terpanjang dari segitiga ini dan bisa dihitung pakai Teorema Pythagoras. Rumus yang dipakai ialah c = akar a² + b², di mana a dan b adalah panjang kedua sisi yang membentuk sudut siku-siku, dan c adalah panjang sisi miring yang ingin kita cari.
Sebagai contoh, jika kita memiliki sebuah segitiga siku-siku dengan panjang sisi-sisi membentuk sudut siku-siku masing-masing 6 cm dan 8 cm, kita dapat rumus tersebut untuk menemukan panjang sisi miringnya. Dengan memasukkan nilai ke dalam rumus, kita mendapatkan c = akar 6² + 8² = akar 36 + 64 = akar 100 = 10. Jadi, panjang sisi miring segitiga tersebut adalah 10 cm. Dengan memahami juga menerapkan rumus ini, kamu dapat mudah menentukan panjang sisi miring pada segala situasi.
Penerapan Rumus Panjang Sisi Miring Segitiga
Setelah tahu rumus panjang bagian miring segitiga ini, kamu mungkin penasaran bagaimana penerapan rumus ini pada kehidupan sehari-hari. Mari simak pada sejumlah poin berikut ini.
- Konstruksi
Penerapan rumus sisi miring segitiga pada kehidupan sehari-hari sangat luas dan berguna. Contohnya ialah dalam bidang konstruksi. Ketika merencanakan pembangunan tangga, misalnya, rumus ini dipakai untuk menentukan panjang tangga yang diperlukan. Dengan mengetahui tinggi tangga serta jarak dari dinding, kamu bisa pakai rumus Pythagoras untuk menghitung panjang tangga supaya aman sesuai standar desain.
- Desain Interior
Selain itu, dalam desain interior, perhitungan panjang sisi miring juga berguna. Misalnya, ketika merancang rak buku melintang di sudut ruangan maupun membuat meja sudut, memahami rumus ini membantu menentukan panjang material yang diperlukan agar sesuai dengan dimensi ruangan juga membuatnya tampak estetik. Dengan cara ini, desain dapat dilakukan dengan presisi, memastikan bahwa hasil akhir fungsional sekaligus harmonis dengan ruang yang ada.
- Teknologi Digital
Di bidang teknologi dan digital, penerapan rumus panjang sisi miring segitiga terlihat dalam pemrograman desain grafis. Ketika membuat grafik model 3D, sering kali kita harus menghitung jarak diagonal antara dua titik dalam ruang. Rumus ini mempermudah perhitungan tersebut, membantu membuat desain lebih akurat sekaligus realistis.
- Olahraga
Pada bidang olahraga, terutama cabang seperti panjat tebing, perhitungan panjang sisi miring penting untuk mengukur jarak yang harus dilalui atlet. Mengetahui panjang tali juga sudut pendakian memungkinkan perencanaan lebih baik dan memastikan keselamatan ketika mendaki. Ini juga berguna untuk merancang jalur pendakian sesuai kemampuan para pendaki.
Kesimpulan
Setelah mempelajari rumus panjang sisi miring segitiga, kamu kini punya alat penting untuk menyelesaikan aneka tantangan matematika dan aplikasinya. Pemahaman baik tentang rumus ini bukan cuma memperkuat dasar pengetahuan geometri kamu, tetapi juga membantu aneka bidang seperti arsitektur juga teknik. Dengan menguasai konsep ini, kamu bisa lebih percaya diri mengaplikasikan prinsip geometri dalam kehidupan sehari-hari. Jangan ragu untuk terus berlatih dan menerapkan rumus panjang sisi miring dalam berbagai situasi praktis ya!